Brownian motion is described by an essentially random motion, which, one of the most famous examples is the movement of a speck of dust floating on the surface of a glass of water.
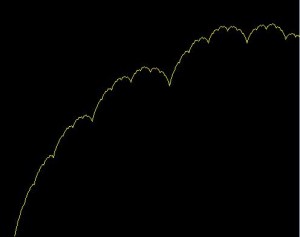
Brownian Motion
For our fractal, the random element of the brownian motion, while essentially still being random is constrained by the end points. To create the fractal, we start with an array of 128 double values. This array could in theory be any size, and is not a fixed requirement.
Now, the first element and last element are our starting and ending points of our path. In the code, these points are randomly generated, but could just as easily be set explicitly.
Before we look at the Generate function, I am going to look at the Gauss function. This function takes three parameters – the seed for the random number generator (so we can create the same fractal by passing the same seed), Mu and Sigma.
The Mu value is the base displacement we want the path to move, and the Sigma value is a multiplier for the random element.
A random number is generated, which is then multiplied by Sigma, which is then added to Mu to give us the displacement of the value for that step in the calculation.
private double Gauss(int iSeed, double fMu, double fSigma)
{
double fx;
int i;
fx = 0;
for (i = 0; i < 12; i++)
{
fx = fx + (new System.Random(iSeed).NextDouble());
}
fx = fx - 6.0;
return fMu + fSigma * fx;
}
The Generate function sets up our arrays, and gets a ratio which will be used as an additional multiplication factor in calculating the movement in each step, using the passed value of H.
Now we begin recursing to set the values of each element of the array.
The last section of the function draws the values which have been generated by the recursion.
public void Generate(Graphics g, double fMu, double fSigma, double fScale, double fH, int fSeed, Color oColor)
{
double fRatio, fStd;
int i;
Pen oPen = new Pen(oColor);
Fh[0] = Gauss(fSeed, fMu, fSigma) * fScale;
Fh[256] = Gauss(0, fMu, fSigma) * fScale;
fRatio = Math.Exp(-0.693147 * fH);
fStd = fScale * fRatio;
Subdivide(0, 255, fStd, fRatio, fMu, fSigma);
for (i = 0; i < 255; i++)
{
g.DrawLine(oPen, 2 * i + 80, 275 - (int)Math.Round(Fh[i]), 2 * (i + 1) + 80, 275 - (int)Math.Round(Fh[i + 1]));
}
}
Now we come to the SubDivide function, which is where the heavy lifting occurs.
Having been passed the starting point and end point, this function calculates the midpoint, and then gets the average of the two points, and then adds the random displacement calculated by the Guass function multiplied by our ratio factor.
We now calculate a new ratio factor, by multiplying the scaled ratio by the original ratio.
Finally, we recursively call Subdivide for the two segments we have now that we have split the original segment into two by finding the midpoint.
If we have reached the point where there are no more points left in-between the end points, we just return, doing nothing, since our job is complete.
private void Subdivide(int f1, int f2, double std, double ratio, double fMu, double fSigma)
{
int fmid;
double stdmid;
fmid = (int)Math.Round((f1 + f2) / 2.0);
if ((fmid != f1) && (fmid != f2))
{
Fh[fmid] = (Fh[f1] + Fh[f2]) / 2.0 + Gauss(0, fMu, fSigma) * std;
stdmid = std * ratio;
Subdivide(f1, fmid, stdmid, ratio, fMu, fSigma);
Subdivide(fmid, f2, stdmid, ratio, fMu, fSigma);
}
}
You can, as usual, get the full source code here.
Comments